了解更多关于自由曲面

常见的光学表面，包括平面、球面、旋转对称非球面和圆柱面，不属于自由曲面的范畴。根据定义，自由曲面是缺少旋转或平移对称约束的光学表面。因此，自由曲面的一个重要特征是它们的不对称性; 它们不是关于任何轴旋转对称的，也不是关于任何平面平移对称的。

自由曲面首先应用于照明领域。随着单点金刚石车削技术的发展，制造各种表面的模具成为可能。然后，这些模具可用于模制或注射模制工艺，以生产满足特定要求的光学表面。与传统元件相比，自由曲面提供了更多的自由度，从而实现了更紧凑的设计、更大的光学视场以及减小的系统重量，从而增强了光学系统的功能。在光学成像领域，自由曲面广泛应用于天文观测和空间光学系统。它们也被结合到一些智能手机镜头中以校正像差。

A.离轴非球面

根据自由曲面的定义，旋转对称非球面的离轴段 (通常称为离轴非球面) 属于自由曲面的范畴。离轴非球面的形状可以是圆形或矩形。

离轴非球面是从原始非球面方程中导出的，其中添加了离轴距离或角度参数。它可以通过数控研磨和抛光制造。

B.环形表面

环形表面，也称为圆环，类似于取自汽车轮胎的一段。它在X和Y方向上弯曲，在两个相互垂直的横截面中具有两个不同的曲率半径。在光学系统中，环形表面具有独特的应用，例如自适应光学系统中的可变形光学元件或红外热成像仪中的扫描元件。在极紫外光谱仪中，环形表面可以用作预镜，以收集更多的光通量。环形表面的形状如下:

假设水平X方向的曲率半径为 (R_x)，圆锥常数为 (K_x)，水平Y方向的曲率半径为 (R_y) 和圆锥常数为 (K_y)，环形曲面的表达式可以表示为:

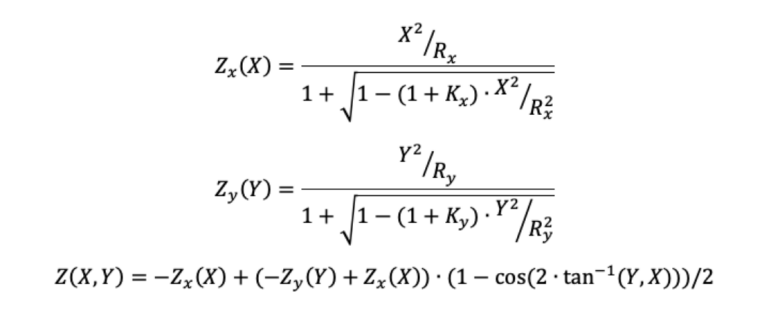
C.XY多项式自由曲面

XY多项式表面通常通过在x和y中添加多项式方程而从非球面表面导出。多项式方程可以是任何形式，包括线性、二次、三次和高阶多项式。这些表面由多个参数控制，通过调整这些参数，可以获得不同的表面形状。

D.Zernike多项式自由曲面

在之前的文章中，我们已经详细介绍了Zernike多项式的概念。Zernike多项式的基函数是连续的，正交的，并且在单位圆内是完整的。每项对应于光学测试中的一种形式的像差，并且正交性确保了每个像差系数的大小与拟合中所使用的项的数量无关。这些特性使Zernike多项式成为自由曲面的理想表示形式，并广泛用于成像光学元件设计。通过在二次曲面上叠加Zernike多项式获得的直径为 (D) 的自由曲面的sag表达式如下:

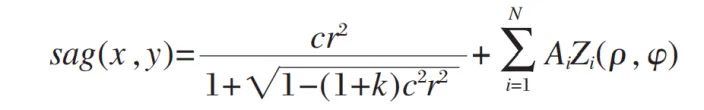
第一个在哪里项表示二次曲面，(k) 是圆锥常数，(c) 是曲率，(r) 是x和y的平方和的平方根，第二项表示泽尼克多项式，(A_i) 是泽尼克多项式系数，(Z_i)是Zernike多项式，(\ rho) 是归一化半径 (r/(D/2) )，(\ phi) 是方位角。

E。Q多项式自由曲面

Q多项式自由曲面是由福布斯从QED光学提出的。这些表面是从Forbes提出的旋转对称Q多项式表面导出的。曲面系数可以直接表示相对于最佳拟合球体的垂度偏差梯度，可用于自由曲面的公差分析。这样可以同时评估光学设计和制造难度，避免了设计后制造评估的繁琐过程。Q多项式的表达式如下:

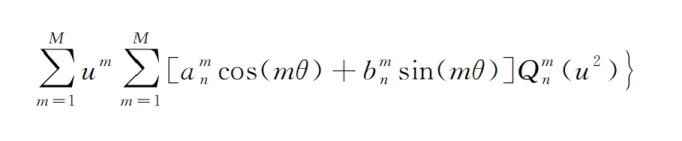
F.非均匀有理b样条 (NURBS) 自由曲面

NURBS曲面通过控制顶点、基函数和每个点的权重的网络来描述曲面。这是用于描述表面的参数化方法。NURBS是国际标准化组织 (ISO) 在STEP标准中定义的用于数据交换的工业产品几何表示的唯一数学方法。调整每个控制点或其权重只会影响该点附近的曲面形状，从而使NURBS成为局部可控的自由曲面。NURBS曲面的表达式很复杂，如下所示:

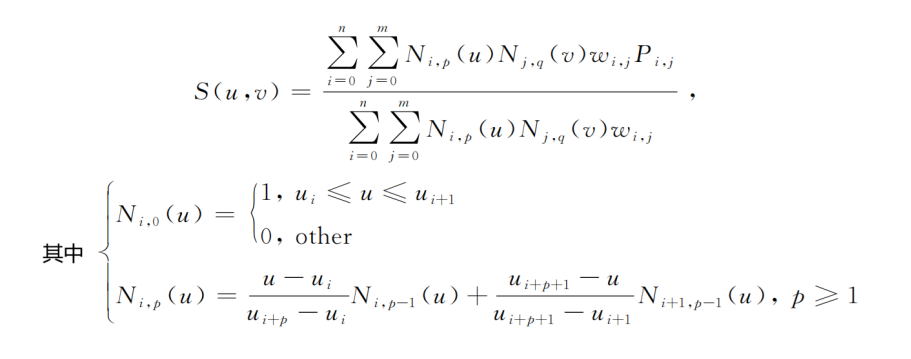
NURBS曲面具有优异的性能，已成功应用于照明领域。然而，大量的变量使得射线追踪极其复杂、耗时且难以优化，限制了其在成像领域的应用。